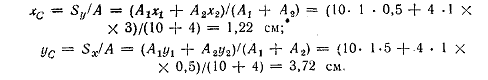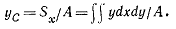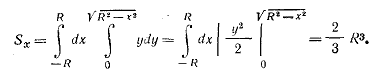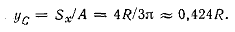|
СОПРОМАТ ОН-ЛАЙН |
 |
Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW - считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн - построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW - эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции - теория, практика, задачи... Справочная информация - ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Книги - разная литература по теме. WIKIbetta |
Базовый курс лекций по сопромату, теория, практика, задачи.:: Посмотреть новый вариант этой лекции:: :: Расчет характеристик он-лайн (программа) :: 1.1. Статический момент сечения.
При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления. Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида
где y - расстояние от элементарной площадки dA до оси x.
Единицей измерения статического момента является единица длины в третьей степени, обычно см3(см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать
где А - площадь всей фигуры (равнодействующая); ус - расстояние от центра тяжести фигуры до оси х. Из формулы (1.2) следует формула определения ординаты центра тяжести ус = Sx/A. (1.3)
Аналогично, статический момент относительно оси у равен
Откуда xс = Sy/A. (1.5)
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии. Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями. Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.
Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю. Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:
Здесь D - облать интегрирования.
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а. Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у. По формулам (1.3) и (1.5) получим:
По этим координатам находим точку С - центр тяести сечения. Она лежит на линии, соединяющей точки С1 и С2, ближе к фигуре, имеющей большую площадь. Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б). Решение. Пользуемся формулой
Вычисляем числитель, используя уравнение окружности х2 + y2 = R2:
Вычисляем ус
1. Пример расчета геометрических характеристик |
СообществоВходРешение задач
Заказать задачу
Профессиональное решение задач в короткие сроки. Расчет редукторовДля Android (рекомендую)Java 2 ME
Mobile Beam 1.6 Программа для расчета балок любой конфигурации на Вашем мобильном телефоне. Новые возможности... Получите код активации бесплатно! |
| © Дмитрий Терехов, 2004-2013. |
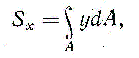 (1.1)
(1.1)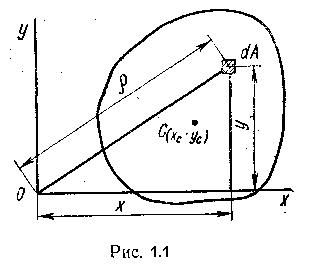
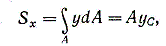 (1.2)
(1.2)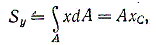 (1.4)
(1.4)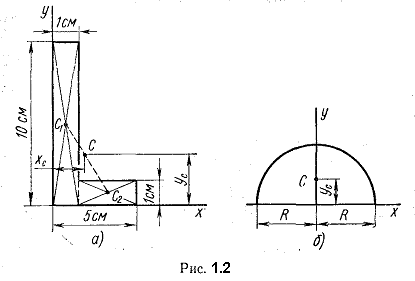
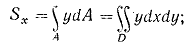 (1.1a)
(1.1a)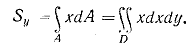 (1.4a)
(1.4a)