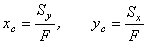СОПРОМАТ ОН-ЛАЙН

Меню сайта Расчет геометрических характеристик сечений он-лайн NEW - считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления. Расчет балок на прочность он-лайн - построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. + Полное расписанное решение! Теперь и для статически неопределимых балок! Расчет рам, ферм балок он-лайн NEW - эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции - теория, практика, задачи... Примеры решения задач Справочная информация - ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги - разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты

<< Назад к списку примеров решения задач Пример №3. Расчет геометрических характеристик сечения. Необходимо рассчитать все основные геометрические характеристики сечения. Расчет выполнен с помощью он-лайн программы на geom.sopromat.org. Площадь сечения F = F1 + F2 - F3; где F1 - площадь прямоугольника 1; F2 - площадь полукруга 2; F3 - площадь круга 3. F1 = h1 x b1 = 10 x 20 = 200 мм2; F2 = PI x R22 : 2 = PI x 102 : 2 = 157.0796 мм2; F3 = PI x R32 = PI x 52 = 78.5398 мм2; F = 200 + 157.0796 - 78.5398 = 278.5398 мм2. Cтатические моменты Обозначим начало координат в самой левой нижней точке сечения. Тогда статический момент сложной фигуры относительно оси Х равен сумме статических моментов простых фигур составляющих эту фигуру. Sx = Sx1 + Sx2 - Sx3; где Sx1 - статический момент прямоугольника 1; Sx2 - статический момент полукруга 2; Sx3 - статический момент круга 3. Sx1 = F1 x Yc1 = 200 x 5 = 1000 мм3; Sx2 = F2 x Yc2 = 157.0796 x 14.2441 = 2237.4575 мм3; Sx3 = F3 x Yc3 = 78.5398 x 10 = 785.398 мм3; Sx = 1000 + 2237.4575 - 785.398 = 2452.0595 мм3. Cтатический момент сложной фигуры относительно оси Y равен сумме статических моментов простых фигур составляющих эту фигуру. Sy = Sy1 + Sy2 - Sy3; где Sy1 - статический момент прямоугольника 1; Sy2 - статический момент полукруга 2; Sy3 - статический момент круга 3. Sy1 = F1 x Xc1 = 200 x 10 = 2000 мм3; Sy2 = F2 x Xc2 = 157.0796 x 10 = 1570.796 мм3; Sy3 = F3 x Xc3 = 78.5398 x 10 = 785.398 мм3; Sy = 2000 + 1570.796 - 785.398 = 2785.398 мм3. Центр тяжести Зная площадь сечения и его статические моменты можно определить координаты центра тяжести по следующим формулам: Xc = 2785.398 : 278.5398 = 10 мм; Yc = 2452.0595 : 278.5398 = 8.8033 мм; Значения координат получены относительно выбранного начала координат O. На схеме центр тяжести обозначен точкой С. Моменты инерции Моменты инерции будем вычислять относительно центральных осей фигуры (центра тяжести). Момент инерции сложной фигуры (Ix) относительно оси Xc (центр тяжести сложной фигуры) равен сумме моментов инерции простых фигур составляющих эту сложную фигуру (относительно этой же оси). Ix = Ix1 + Ix2 - Ix3; где Ix1 - момент инерции прямоугольника 1; Ix2 - момент инерции полукруга 2; Ix3 - момент инерции круга 3. Ix1 = Ix1' + b12 x F1; Ix2 = Ix2' + b22 x F2; Ix3 = Ix3' + b32 x F3; где Ix1' - момент инерции прямоугольника 1 относительно собственного центра тяжести; Ix2' - момент инерции полукруга 2 относительно основания; Ix3' - момент инерции круга 3 относительно собственного центра тяжести; b1 - расстояние от центра тяжести прямоугольника 1 до оси Xc (по оси Yc); b2 - расстояние от основания полукруга 2 до оси Xc (по оси Yc); b3 - расстояние от центра тяжести круга 3 до оси Xc (по оси Yc); F1 - площадь прямоугольника 1; F2 - площадь полукруга 2; F3 - площадь круга 3. Ix1' = b1 x h13 : 12 = 1666.6667 мм4; Ix2' = PI x D24 : 128 = 3926.9908 мм4; Ix3' = PI x D34 : 64 = 490.8739 мм4; Ix1 = 1666.6667 + 3.80332 x 200 = 4559.6849; Ix2 = 3926.9908 + 1.19672 x 157.0796 = 4151.9431; Ix3 = 490.8739 + 1.19672 x 78.5398 = 603.35; Ix = 4559.6849 + 4151.9431 - 603.35 = 8108.278 мм4. Момент инерции сложной фигуры (Iy) относительно оси Yc (центр тяжести сложной фигуры) равен сумме моментов инерции простых фигур составляющих эту сложную фигуру (относительно этой же оси). Iy = Iy1 + Iy2 - Iy3; где Iy1 - момент инерции прямоугольника 1; Iy2 - момент инерции полукруга 2; Iy3 - момент инерции круга 3. Iy1 = Iy1' + a12 x F1 мм4; Iy2 = Iy2' + a22 x F2 мм4; Iy3 = Iy3' + a32 x F3 мм4; где Iy1' - момент инерции прямоугольника 1 относительно собственного центра тяжести; Iy2' - момент инерции полукруга 2 относительно основания; Iy3' - момент инерции круга 3 относительно собственного центра тяжести; a1 - расстояние от центра тяжести прямоугольника 1 до оси Yc (по оси Xc); a2 - расстояние от основания полукруга 2 до оси Yc (по оси Xc); a3 - расстояние от центра тяжести круга 3 до оси Yc (по оси Xc); F1 - площадь прямоугольника 1; F2 - площадь полукруга 2; F3 - площадь круга 3. Iy1' = h1 x b13 : 12 = 6666.6667 мм4; Iy2' = PI x D24 : 128 = 3926.9908 мм4; Iy3' = PI x D34 : 64 = 490.8739 мм4; Iy1 = 6666.6667 + 02 x 200 = 6666.6667; Iy2 = 3926.9908 + 02 x 157.0796 = 3926.9908; Iy3 = 490.8739 + 02 x 78.5398 = 490.8739; Iy = 6666.6667 + 3926.9908 - 490.8739 = 10102.7836 мм4. Моменты сопротивления Осевым моментом сопротивления площади сечения относительно главной центральной оси называется отношение момента инерции площади относительно этой же оси к расстоянию до наиболее удаленной точки от этой оси. Wx = Ix : Ymax = 8108.278 : 11.1967 = 724.1668 мм3; Wy = Iy : Xmax = 10102.7836 : 10 = 1010.2784 мм3. Полезные ссылки Программа для расчета геометрических характеристик любых сечений он-лайн.

Сообщество Поиск людей Вход Логин: Пароль: Регистрация Забыли пароль? Решение задач Заказать задачу Профессиональное решение задач в короткие сроки. Расчет редукторов Расчет редуктора он-лайн Расчет любого редуктора он-лайн. Записка + чертежи Для Android (рекомендую) NEW Mobile Beam 2.0 Программа для расчета балок на прочность на Вашем Android устройстве... Java 2 ME Mobile Beam 1.6 Программа для расчета балок любой конфигурации на Вашем мобильном телефоне. Новые возможности... Получите код активации бесплатно! Сообщить другу по СМС (бесплатно) Скачать Mobile Beam по СМС (бесплатно)

© Дмитрий Терехов, 2004-2013.