|
СОПРОМАТ ОН-ЛАЙН |
 |
Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW - считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн - построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW - эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции - теория, практика, задачи... Справочная информация - ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Книги - разная литература по теме. WIKIbetta |
Базовый курс лекций по сопромату, теория, практика, задачи.1.3. Моменты инерции простых сечений.
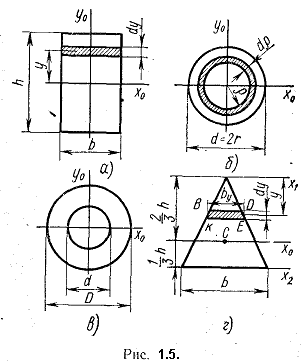
1. Прямоугольник (рис. 1.5,а). Вычислим момент инерции сечения относительно оси Х0, проходящей через центр тяжести параллельно основанию. За dA примем площадь бесконечно тонкого слоя dA = bdy.
Тогда
Аналогично, получим
2. Круг (рис. 1.5,б). Сначала определим полярный момент инерции относительно центра круга
За dA принимаем площадь бесконечно тонкого кольца толщиной dp
тогда
Следовательно,
Теперь легко найдем Ixo. Действительно, для круга согласно формуле (1.9.), имеем Iр = 2Iхо = 2Iуо, откуда
2. Кольцо (рис. 1.5,в). Осевой момент инерции в этом случае равен разности моментов инерции внешнего и внутреннего кругов
Аналогично полярный момент инерции
2. Треугольник (рис. 1.5,г). Определим момент инерции относительно оси x1, параллельной основанию и проходящей через вершину треугольника
За dA примем площадь бесконечно тонкой трапеции KBDE, площадь которой можно считать равной площади прямоугольника: Легко получить из подобия треугольников Определим момент инерции относительно центральной оси; для этого используем формулу (1.10)
Определим момент инерции относительно оси, проходящей через основание:
|
СообществоВходРешение задач
Заказать задачу
Профессиональное решение задач в короткие сроки. Расчет редукторовДля Android (рекомендую)Java 2 ME
Mobile Beam 1.6 Программа для расчета балок любой конфигурации на Вашем мобильном телефоне. Новые возможности... Получите код активации бесплатно! |
| © Дмитрий Терехов, 2004-2013. |
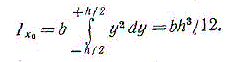
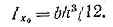 (1.11)
(1.11)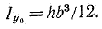 (1.12)
(1.12)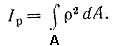
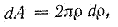
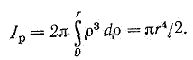
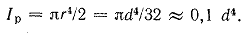 (1.13)
(1.13)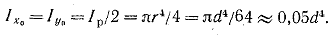 (1.14)
(1.14)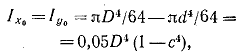 (1.15)
(1.15)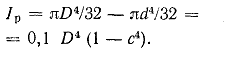 (1.16)
(1.16)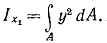
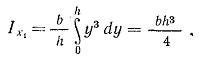 (1.17)
(1.17)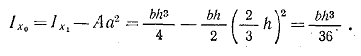 (1.18)
(1.18)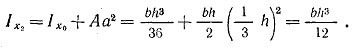 (1.19)
(1.19)