Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW - считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн - построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW - эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции - теория, практика, задачи...
Примеры решения задач
Справочная информация - ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Форум сопромата и механики
Книги - разная литература по теме.
Заказать задачу
Друзья сайта (ссылки)
WIKIbetta
Разработчикам (сотрудничество)
Веб-мастерам (партнёрка)
О проекте, контакты
Подпроекты
|
Форум >> Нужна помощь >> Помощь студентам тут

|
|
|
|
Не смущайтесь того что пока мало записей!!
Ведь форум сейчас переезжает с сайта sopromat.org сюда...
|
|
08 ноября 2008 г. в 13:54
|
|
|
|
|
|
|
|
Допоможіть розвязати задачу
|
|
08 ноября 2008 г. в 14:01
|
|
|
|

|
|
|
|
Давай помогу))
|
|
09 ноября 2008 г. в 11:16
|
|
|
|

|
|
|
|
|
|
12 ноября 2008 г. в 15:03
|
|
|
|

|
|
|
|
Прошу оказать помощь в решении задач, точнее говоря
нужна подсказка...
Есть балка на ней распределенные нагрузки (по треугольнику),
собственно есть и другие но сними проблем нет :),
как составить аналитические выражения для Q и M ?
При проходе участков балки слева-направо и справа-налево,
для распределенной нагрузки изменяющейся по треугольнику от
0 до q и наоборот от q до 0.
PS Фотку при случае вставлю :)
Александр.
|
|
12 ноября 2008 г. в 15:13
|
|
|
|

|
|
|
|
все просто!! особенно когда от 0 до q или наоборот))
при расчете, можно упростить так:
считать, что нагрузка не по треугольнику, а прямоугольная, тогда ее значение будет пополам. А вектор приложения нагрузки остается также по середине, как и при прямоугольной ))
|
|
12 ноября 2008 г. в 15:25
|
|
|
|

|
|
|
|
эту тему дообсуждаем, а в дальнейшем новый вопросы прошу задавать в отдельно созданных темах.
|
|
12 ноября 2008 г. в 15:25
|
|
|
|

|
|
|
|
А вектор приложения нагрузки остается также по середине, как и при прямоугольной
А я думал что что через центр тяжести треугольника...
Когда изменяется от 0 до q еще могу записать, а когда наоборот
думал что нужно "трапецию" на прямоугольник и треугольник разложить...
На выходных попробую посчитать и посмотреть что выйдет.
Большое спасибо за совет.
|
|
13 ноября 2008 г. в 07:11
|
|
|
|

|
|
|
|
да да да, оговорился... центр тяжести
|
|
13 ноября 2008 г. в 17:48
|
|
|
|

|
|
|
|
а что рассчитываешь? задачу??
или что то реальное с такой неравонмерной нагрузкой? ))
|
|
13 ноября 2008 г. в 18:13
|
|
|
|

|
|
|
|
очень интересно ))
|
|
02 декабря 2008 г. в 21:32
|
|
|
|

|
|
|
|
Сосед мой на старости лет подался в студенты...
Толковый мужик,а для должности гл.механика ему необходимо
высшее образование. Вот он меня и терзает своими задачами.
А я сопромат учил последний раз в 1988 году, и конспектов
своих уже давно нет... Кое что еще помню, кое что вспоминаю
когда открываю книгу.
Сейчас заново разбираюсь со статически определимыми рамами,
пока еще мои эпюры "отличаются" от эпюр програмы "Полюс" :(
|
|
03 декабря 2008 г. в 06:39
|
|
|
|

|
|
|
|
Sorry ! Login не ввел.
А получилось что под чужим ником ответил ...
|
|
03 декабря 2008 г. в 06:48
|
|
|
|

|
|
|
|
в программе полюс есть ошибки кстати ((..
хороша прога...
я обратил внимание, что в некоторых случаях момент не учитывается((... в каких точно сейчас не скажу...
|
|
03 декабря 2008 г. в 11:25
|
|
|
|

|
|
|
|
Опа ! И у меня как раз с моментом вопрос.
Когда момент ставлю на "подвижную опору" он "не учитывается"
при определении реакций опор. Вторая опора шарнир.
Если "передвигаю" момент на другой узел - реакции
считаются верно.
А может момент игнорируется потому что я его на
"подвижную" опору назначаю ?
|
|
04 декабря 2008 г. в 07:30
|
|
|
|

|
|
|
|
не могу сказать, давно не ользовался прогой...
вообще какая разница подвижная или нет ... ведь если стержень устойчивый, то любая приложенная нагрузка должна вызывать внутреннее напряжение....
|
|
04 декабря 2008 г. в 12:38
|
|
|
|

|
|
|
|
Помогите,нужна помощь для решение статически неопределимого бруса и статически неопределимой системы,если кто знает,то с радостью отправлю чертёж и условие. Обещаю вознагрождение!
|
|
04 декабря 2008 г. в 16:29
|
|
|
|

|
|
|
|
Привет, что случилось со старой системой? Договорился на счёт решения задачи, и теперь не могу найти с кем именно.
Anna, напишите, если увидите сообщение.
|
|
08 декабря 2008 г. в 10:18
|
|
|
|

|
|
|
|
Я тебе сейчас напишу в личку ее адрес
|
|
08 декабря 2008 г. в 10:23
|
|
|
|

|
|
|
|
Народ!!! помогите .. не знаю как решить задачу по сопромату по теме --плоская рама--может кто поможет !!!по рисунок [URL=http://pixs.ru/?ref=120875][IMG]http://img.pixs.ru/images/prarbmp_1441013_120875.bmp[/IMG][/URL] Кто сможет решить скиньте плиз решение на мыло upling@narod.ru Заранее спасибо.
|
|
08 декабря 2008 г. в 14:12
|
|
|
|

|
|
|
|
обведи конструкцию пожирнее, а то не очень понятно
|
|
08 декабря 2008 г. в 22:45
|
|
|
|

|
|
|
|
Помогите, пожалуйста, решить задачу.
Нужно построить эпюры Mz и Qy.
И, по возможности, объясните мне, как это делается.
Рисунок: http://s57.radikal.ru/i156/0812/68/a9c94e2e1fec.jpg
|
|
09 декабря 2008 г. в 08:59
|
|
|
|

|
|
|
|
горохов откликнись
|
|
09 декабря 2008 г. в 13:09
|
|
|
|

|
|
|
|
все очень просто.
нужно только в общем виде решить? или в численом тоже?
для численного решения не хватает значения q.
создай отдельную тему с этим вопросом я расскажу
|
|
09 декабря 2008 г. в 13:10
|
|
|
|

|
|
|
|
Хорошо. А как тему то назвать?
|
|
09 декабря 2008 г. в 13:22
|
|
|
|

|
|
|
|
))
как хочешь, например "Нужно построить эпюры Mz и Qy."
|
|
09 декабря 2008 г. в 13:41
|
|
|
|

|
|
|
|
Уже создала. Жду.
|
|
09 декабря 2008 г. в 13:56
|
|
|
|
Подписаться на новые сообщения этой темы
Инфо форума
Администратор форума: Krolist
|
|
Сообщество
Вход
Решение задач
Расчет редукторов
Для Android (рекомендую)
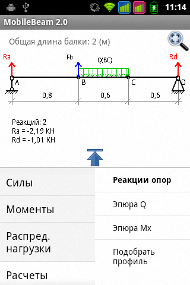
 NEW Mobile Beam 2.0
NEW Mobile Beam 2.0Программа для расчета балок на прочность на Вашем Android устройстве...
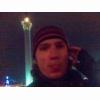
Java 2 ME

|